131 private links
The set of all points closest to a given point in a point set than to all other points in the set is an interesting spatial structure called a Voronoi Polygon for the point. The union of all the Voronoi polygons for a point set is called Voronoi Tessellation.
Many applications have been found based on the neighbourhood information provided by this tessellation. The dual of Voronoi tessellation is Delaunay Tessellation, also referred to as Delaunay Triangulation or Triangulated Irregular Network (TIN), which are lines drawn between points where their Voronoi polygons have an edge in common.
Delaunay tessellation is the most fundamental neighbourhood structure because many other important neighbourhood structures, such as, Gabriel Graph, Relative Neighbourhood Graph and Minimal Spanning Tree, can be derived from it.
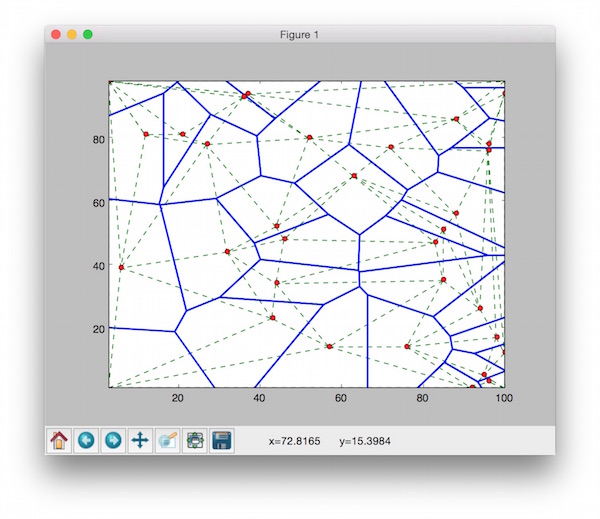
We shall introduce PyDelaunay as a practical spatial construction. It is an efficient Python implementation of Voronoi/Delaunay Tessellation, which can be served as the Basic Map of the neighbourhood concept.

Joy as mathematicians discover a new type of pentagon that can cover the plane leaving no gaps and with no overlaps. It becomes only the 15th type of pentagon known that can do this, and the first discovered in 30 years.
