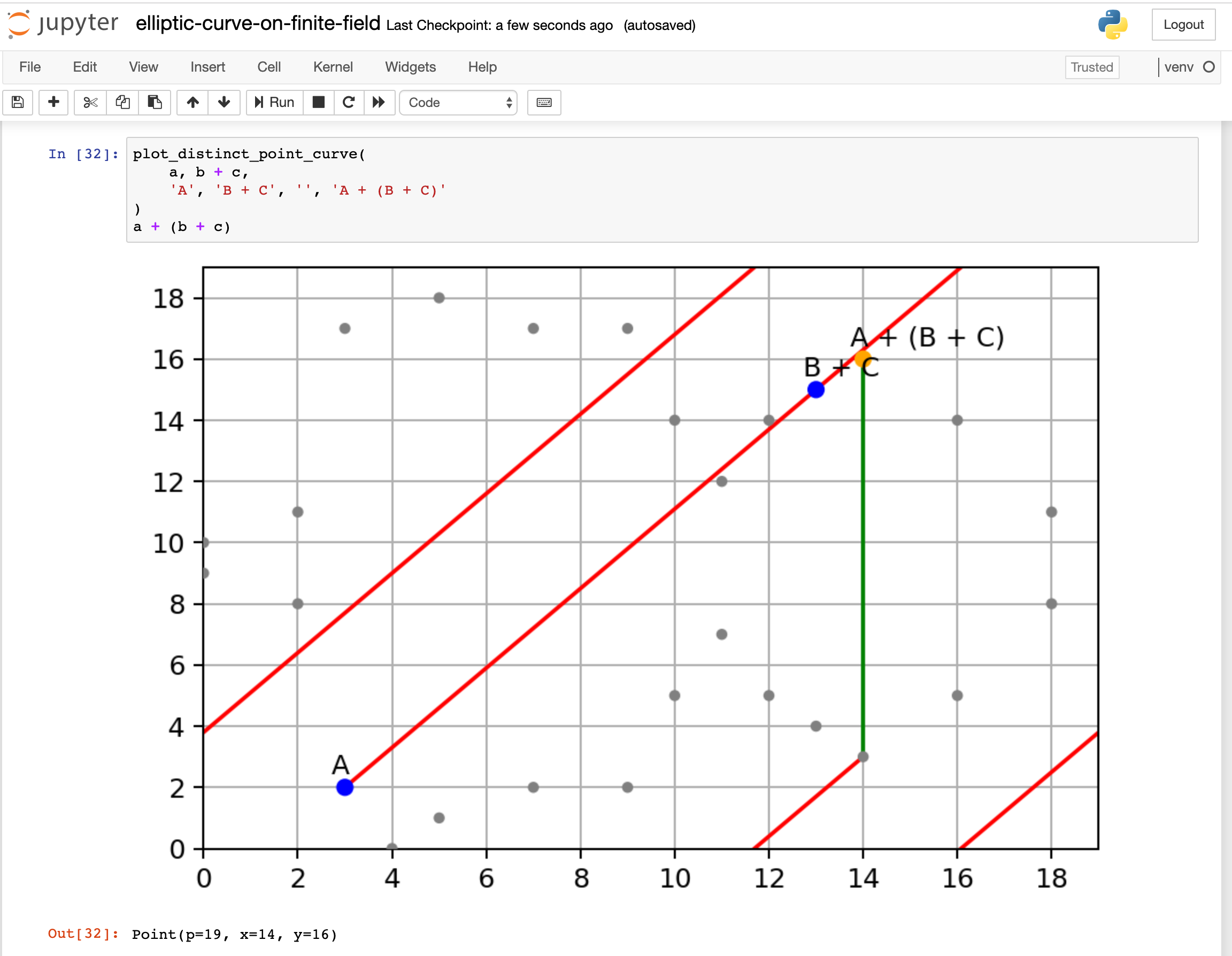
Recently, I am learning how Elliptic Curve Cryptography works. I searched around the internet, found so many articles and videos explaining it. Most of them are covering only a portion of it, some of them skip many critical steps how you get from here to there. In the end, I didn’t find an article that really explains it from end-to-end in an intuitive way.
With that in mind, I would like to write a post explaining Elliptic Curve Cryptography, cover from the basics to key exchange, encryption, and decryption.
— Permalink]]>